
Let's see, if I stick in 5, is it true that zero is greater than 2 times 7? No.

I'm going if I can use any value I want to and if there's a solution, then every value out here would be a solution. If 5 works, and so should every single number that's bigger than 3. I'm going to pick another x number out here. I'm going to be shading at least that piece and perhaps even more I got to test this last chunk of my line graph. Yes, that means this middle part is a solution. When I substitute zero in here I want to see if I get a true inequality. I just chose zero because zeroes for me are pretty easy to work with. But I need to test this region as well in between my two open circles. 13 times -8 is a positive answer, right? So no this would not be part of my solution region. Well, if my x number were equal to -10 and I substituted in there, I want to see whether or not I get a true inequality. Any value less than -2, I'm going to test this region. Like what would happen if I were to pick an x value out here? Like let's say I chose x is equal to -10. Then what I'm going to do is pick test points, a lot like what you do when you're graphing linear inequalities on the xy plane, this is the same idea. Well I'm going to go ahead and stick open circles on those guys based on this inequality sign.
#SOLVING QUADRATIC INEQUALITIES HOW TO#
I'm going to have to think about open circles and closed circles as well as how to shade my solution region. Okay, what happens all around them is what's going to be important. I'm going to stick those guys on a number line. We already know that the x intercepts will be at -2 and +3. Well the first thing you're going to be looking for is the places where you have x intercepts. How would you do this if all you had was this original problem statement? So what we're going to be working on and what you guys will be doing in your homework is how to do these problems without a graph. You don't want to have to draw the picture. But a lot of times you guys I know graphing quadratics is a real drag. So that's one way to do it if you have the graph. Notice I'm using strict less than signs, I'm not using equal than or equal to because of this guy here. So we're looking for where is this graph less than zero and if you are to look at this picture, looking at this picture you can tell pretty easily the places where the graph is less than zero is this whole region down here or for x values that are in between -2 and +3. Let me rewrite that with a better marker, like that, okay. What you're going to be looking at is equations that look a lot like this only instead of y equals you're going to have some kind of inequality business. This has intercepts of -2 and +3 on the x axis and then the parabola shape opens upward. This is already in factored form right? Check out the graph here. Think about the equation y equals the quantity x-3 times x+2.
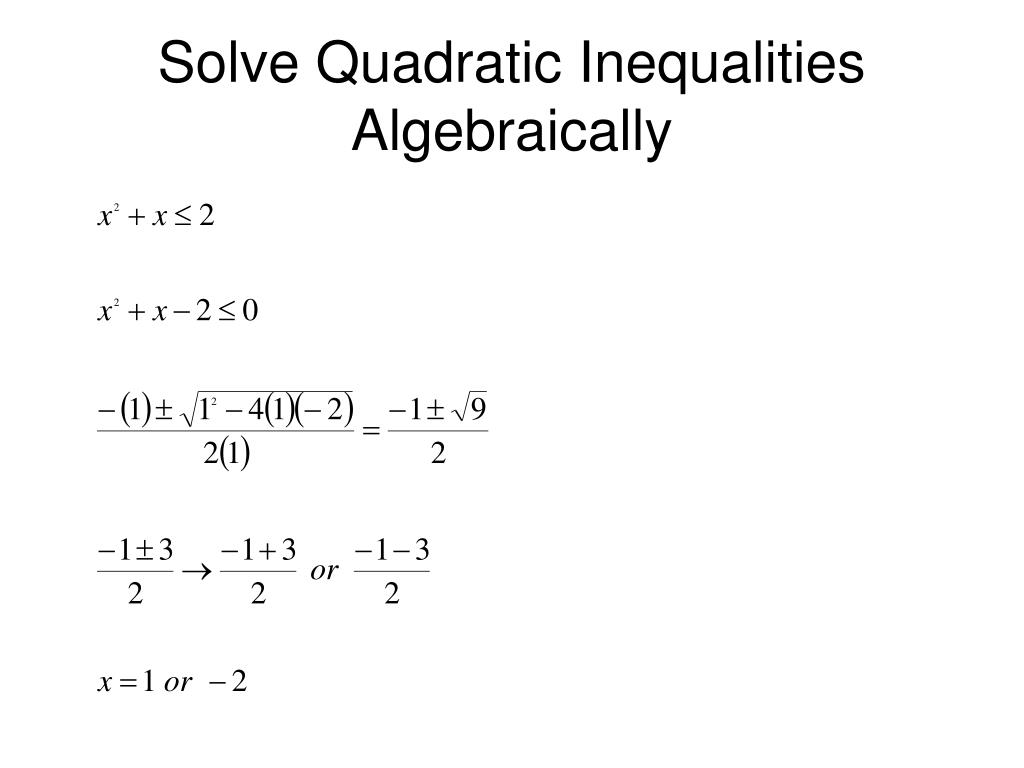
See the Inequalities Calculators by iCalculator™ below.When we're looking at quadratic inequalities, one of the things you want to keep in mind is what you know about graphs of quadratics.
#SOLVING QUADRATIC INEQUALITIES FULL#

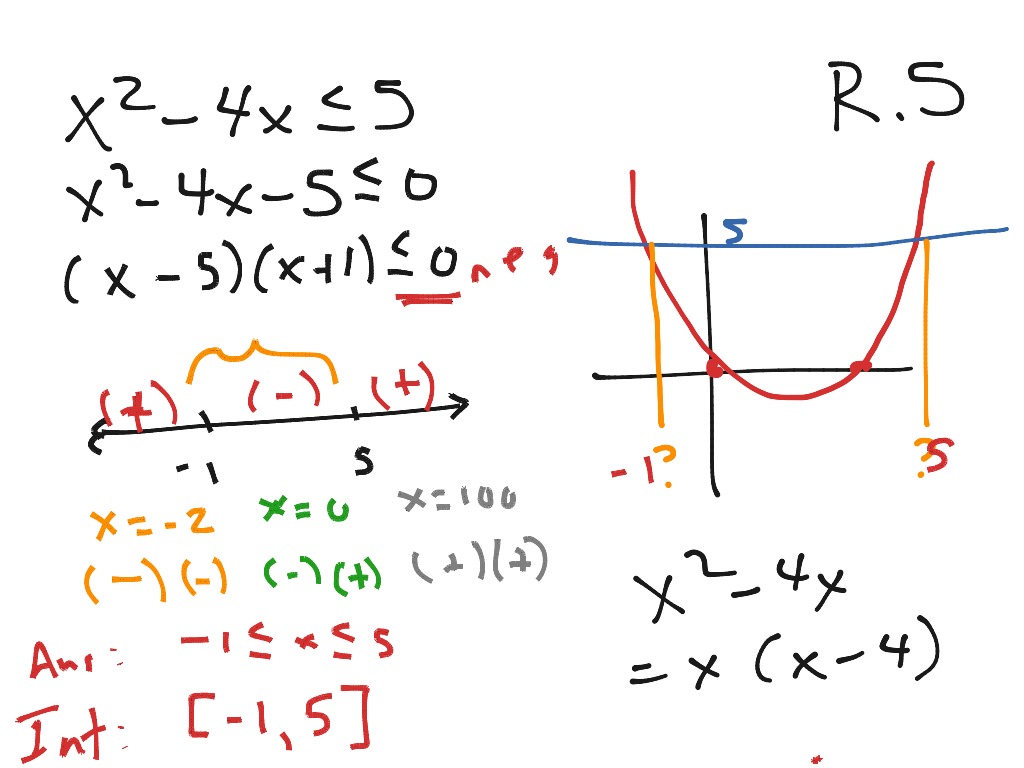
Read the Quadratic Inequalities math tutorial and build your math knowledge of Inequalities Inequalities Math tutorial: Quadratic Inequalities.Helps other - Leave a rating for this solving (see below) Solving Quadratic Inequalities by Studying the SignĮnjoy the "Solving Quadratic Inequalities" math lesson? People who liked the "Quadratic Inequalities lesson found the following resources useful: 8 ≥ 0 (true) More Quadratic Inequalities Lessons and Learning Resources Inequalities Learning Material Tutorial ID


 0 kommentar(er)
0 kommentar(er)
